

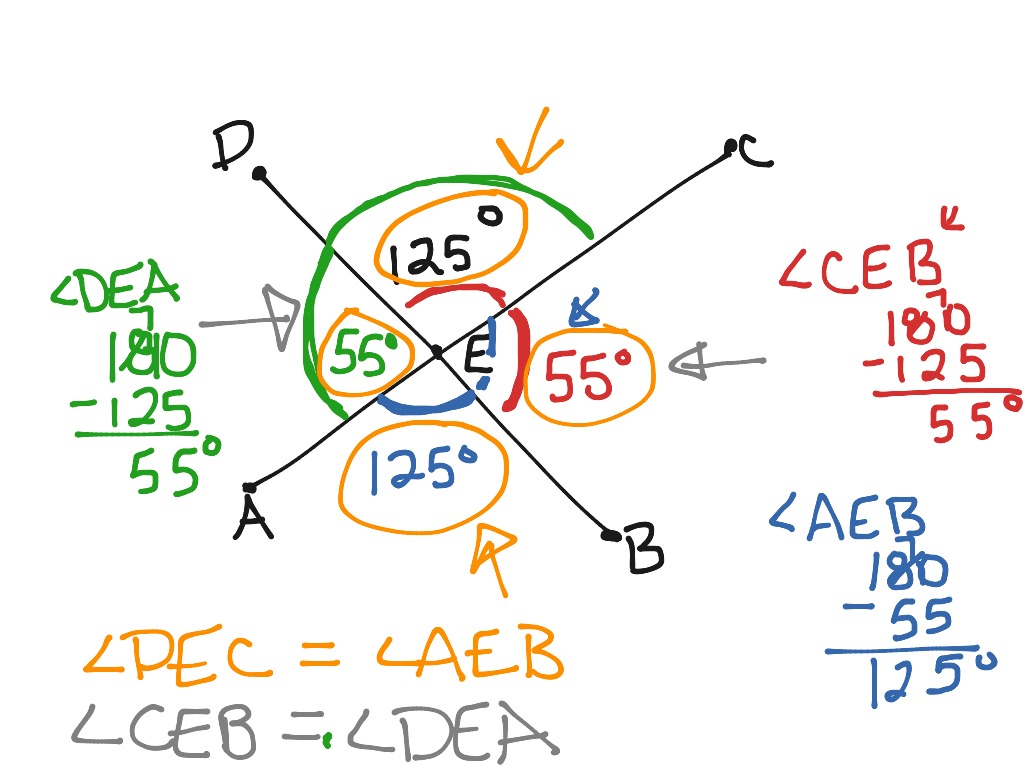
Since ∠c is vertical to ∠a (and because vertical angles are congruent), ∠c also equals 135.įurthermore, since ∠b is supplementary to ∠a, their sum must equal 180. So, if for example, you only that ∠a=135, you could use the Vertical Angles Theorem to figure out the angle measures of ∠b, ∠c, and ∠d. Furthermore, any combination of a pink angle and a green angle will be a linear pair (supplementary) and they will have a sum of 180. So, the green angles ∠a and ∠c are congruent, as well as the pink angles, ∠d and ∠b. Namely, that the two pairs of vertical angles formed are congruent.Īgain, when two straight lines intersect, the vertical angles that are formed are always congruent (or equal) to each other. The Vertical Angles Theorem states that whenever two straight lines intersect, they form two sets of supplementary angles (linear pairs) that are congruent to each other.
#VERTICAL ANGLES GEOMETRY DEFINITION HOW TO#
Now that you understand how to identify vertical angles and why vertical angles are always congruent, you are ready for the Vertical Angles Theorem. So, are vertical angles congruent? Yes! Vertical angles are congruent, meaning that they always have the same degree measure.
∠AEC and ∠DEA are a linear pair and they combine to equal 180 (salmon-colored and purple-colored combo)ĬEB and ∠DEB are a linear pair and they combine to equal 180 (salmon-colored and purple-colored combo)
∠CEB and ∠DEA are vertical angles and they both equal 60 (they are both purple-colored) ∠AEC and ∠DEB are vertical angles and they both equal 120 (they are both salmon-colored) The two pairs of vertical angles both have the same measure. Notice that there are four total angles: ∠AEC, ∠DEA, ∠DEB, and ∠CEB Take a look at the two intersecting lines shown in Figure 1 below. Vertical angles are the pairs of angles that are opposite (or directly across from) each other that are made by two intersecting lines. In math, you often have to be able to classify angles and angle relationships that are formed by two intersecting lines. You will also be able to identify an example of a vertical angle given a diagram (this guide includes three vertical angles examples and practice problems at the end). Once you learn the answer to these three questions, you will be able to understand the properties of vertical angles and solve math problems that involve vertical angles. In this short guide, we will explore and answer the questions: One of the most common angle relationships that you will come across are vertical angles, or angles that are directly opposite each other. When studying mathematics-namely the field of Geometry-it is incredibly important to understand the properties of angles and angle relationships.


 0 kommentar(er)
0 kommentar(er)
